开始之前,先解释一下一些基本的术语,比如方差(variance)、标准差(standard deviation)、正态分布(normal distribution)、估计(estimate)、准确率(accuracy)、精度(precision)、均值(mean)、期望(expected value)和随机变量(random variable)。
假设大部分读者已经了解基本的统计知识。但是在开始之前,还是简单的介绍一下理解卡尔曼滤波的基本概念。如果你熟悉这些内容,可以跳过此部分。
均值和期望
均值和期望非常相似,但是却并不相同。
比如,有5个硬币,2个5分和3个10分,那么可以很容易计算出这些硬币的平均值:
$$ V_{\text {mean}}=\frac{1}{N} \sum_{n=1}^{N} V_{n}=\frac{1}{5}(5+5+10+10+10)=8 $$
由于系统状态(硬币值)是确定的,没有隐藏信息,而且使用了所有的信息计算平均值。因此,上述结果不能定义为期望。
假设测量了一个人的5次体重信息:79.8kg, 80kg, 80.1kg, 79.8kg, 和 80.2kg。
由于秤测量时存在随机测量误差,所以每次测量结果都不同。因为存在隐含变量(Hidden Variable),我们不知道体重的真实值究竟是多少。但是可以通过计算测量的平均值估计体重。
$$ W=\frac{1}{N} \sum_{n=1}^{N} W_{n}=\frac{1}{5}(79.8+80+80.1+79.8+80.2)=79.98 k g $$
估计的输出就是体重的期望。均值通常通过 $\mu$ 表示,期望通常通过 $E$ 表示。
方差和标准差
方差是衡量数据集偏离平均值的程度。标准差是方差的均方根,通常通过 $\sigma$ 表示,而方差通过 $\sigma^2$ 表示。
比如,我们想对比两个篮球队的身高,下面是两个篮球队的队员的身高和平均值信息:
$$ \begin{aligned}\begin{array}{lllllll} & \text { Player 1 } & \text { Player 2 } & \text { Player 3 } & \text { Player 4 } & \text { Player 5 } & \text { Mean } \\hline \text { Team A } & 1.89 \mathrm{m} & 2.1 \mathrm{m} & 1.75 \mathrm{m} & 1.98 \mathrm{m} & 1.85 \mathrm{m} & 1.914 \mathrm{m} \\hline \text { Team B } & 1.94 \mathrm{m} & 1.9 \mathrm{m} & 1.97 \mathrm{m} & 1.89 \mathrm{m} & 1.87 \mathrm{m} & 1.914 \mathrm{m}\end{array}\end{aligned} $$
由上可知,两个队的平均身高相同。下面看一下各自的身高方差。因为方差衡量的是数据集的离散程度,我们需要知道数据集偏离均值的程度。我们可以通过将每个值减去均值计算每个值到均值的距离。
我们使用 $x$ 表示身高,$\mu$ 表示均值,每个变量到均值的距离为:
$$ x_{n}-\mu=x_{n}-1.914 m $$
下表表示的是每个变量到均值的距离:
$$ \begin{aligned}\begin{array}{llllll} & \text { Player 1 } & \text { Player 2 } & \text { Player 3 } & \text { Player 4 } & \text { Player 5 } \\hline \text { TeamA } & -0.024 \mathrm{m} & 0.186 \mathrm{m} & 0.164 \mathrm{m} & 0.066 \mathrm{m} & -0.064 \mathrm{m} \\hline \text { Team B } & 0.026 \mathrm{m} & .0 .014 \mathrm{m} & 0.056 \mathrm{m} & 0.024 \mathrm{m} & -0.044 \mathrm{m}\end{array}\end{aligned} $$
有些值是负的,为了消除负值的影响,对每个值求平方:
$$ \left(x_{n}-\mu\right)^{2}=\left(x_{n}-1.914 m\right)^{2} $$
下表表示的是每个变量到均值的距离的平方:
$$ \begin{aligned}&\begin{array}{llllll} & \text { Player 1 } & \text { Player 2 } & \text { Player 3 } & \text { Player 4 } & \text { Player 5 } \\hline \text { Team A } & 0.000576 \mathrm{m}^{2} & 0.034596 \mathrm{m}^{2} & 0.026896 \mathrm{m}^{2} & 0.004356 \mathrm{m}^{2} & 0.004096 \mathrm{m}^{2} \\hline \text { Team B } & 0.000676 \mathrm{m}^{2} & 0.000196 \mathrm{m}^{2} & 0.003136 \mathrm{m}^{2} & 0.000576 \mathrm{m}^{2} & 0.001936 \mathrm{m}^{2}\end{array}\end{aligned} $$
为了计算数据集的方差,需要计算所有变量到均值的距离的平方的均值:
$$ \sigma^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2} $$
第一队的方差为:
$$ \sigma_{A}^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}=\frac{1}{5}(0.000576+0.034596+0.026896+0.004356+0.004096)=0.014 m^{2} $$
第二队的方差为:
$$ \sigma_{B}^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}=\frac{1}{5}(0.000676+0.000196+0.003136+0.000576+0.001936)=0.0013 m^{2} $$
尽管两个队身高的均值相同,但是第一队的身高的离散程度比第二队要大,表明:第一队的人员身高更分散,更适合分配到不同的位置,而第二队身高相近,可能不利于站位的分配。
方差的单位是平方,所以使用标准差更方便对比。标准差是方差的均方根。
$$ \sigma=\sqrt{\frac{1}{N} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}} $$
第一队的标准差是0.12m,第二队的标准差是0.036m。
现在,假设我们要计算所有高中所有篮球队员身高的方差和均值。我们就需要收集所有高中所有篮球队员的身高数据,这是相当困难的。
但是,我们可以从大量数据集中选择一部分数据计算方差和均值,估计所有数据的方差和均值。对于准确估计队员身高的方差和均值来说,选择100个篮球队员的信息就足够了。
然而在估计方差时,方差的计算方式有所不同。使用$N - 1$ 代替 $N$ 进行归一化计算:
$$ \sigma^{2}=\frac{1}{N-1} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2} $$
数学证明可以参考:Here
正态分布
很多自然现象都遵循**正态分布(Normal Distribution)。比如上面提到的篮球队员的身高,如果从从大量的数据集中随机选择一定的数据,然后绘制身高出现的频次,可以得到一个钟形曲线,如下图所示:
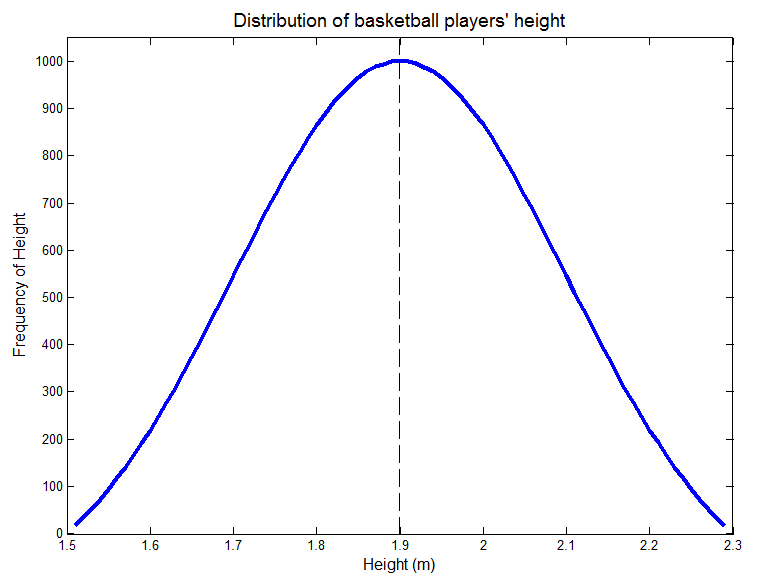
如图所示,钟形曲线是关于均值对称的。均值周围的数据出现的频次比两边的值出现的频次更高。
高度的标准差等于0.2 m。68.26%的值出现在均值的一个标准差范围内,即68.26%的值在1.7 m到2.1 m之间,下图绿色区域。
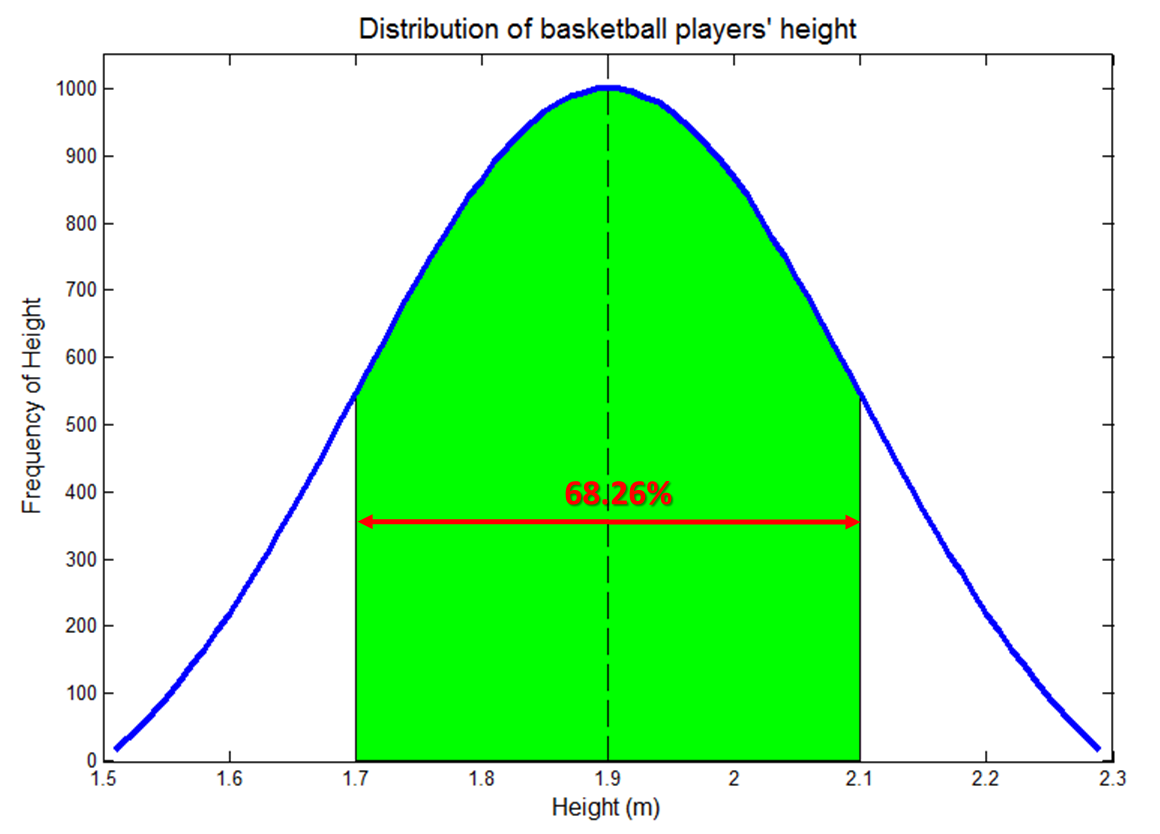
95.44%的值出现在均值的两个标准差范围内,99.74%的值出现的均值的三个标准差范围内。
正态分布也称为高斯分布,通常通过如下等式表示:
$$ f\left(x ; \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}}} $$
高斯曲线也称为正态分布的概率密度函数(Probability Density Function,PDF)。
通常,测量误差服从正态分布。卡尔曼滤波假设测量误差服从正态分布。
随机变量
一个数学家、物理学家和工程师的车速为60 km/h。警察拦停了他们,并利用激光测速仪进行了测速,测量结果为 70 km/h。测速仪的测量结果服从正态分布,且方差为 5 km/h。
测速仪的测量结果就是随机变量。我们不知道准确的速度,速度的期望是70 km/h。
数学家说:速度可以是负无穷到正无穷,但是速度在65到75 km/h的概率为68.6%。
物理学家说:速度是任何大于负的光速且小于正的光速的值。
工程师说:速度可以是任何大于0小于140 km/h的值。因为移动方向是向前的,而且车速最高140 km/h。
警察说车速是70 km/h,并给了一张罚单。
随机变量可以是连续的或离散的:
- 电池的消耗时间或马拉松的时间是连续随机变量;
- 网站访问者或班级的学生数是离散的。
估计、准确率和精度
估计(estimate) 是对系统隐藏状态的评估。对于观测者来说,飞机的真正位置就是隐藏变量。我们可以使用传感器,比如雷达,估计飞机的位置。使用多传感器和高级的估计和追踪算法,比如卡尔曼滤波,可以显著改善估计的结果。每个测量或计算参数都是估计值。
准确率(accuracy) 表示测量和真实值间的距离。
精度(precision) 描述的是相同参数下测量的离散程度。准确率和精度是估计的基础。
下图很好的解释了准确率和精度:

高精度系统的测量具有低方差,即低不确定性,然而低精度系统的测量具有高方差,即高不确定性。方差是由随机测量误差所产生。
低准确率系统称为有偏系统,因为其测量具有系统性误差(systematic error)。
通过平均或平滑测量可以显著降低方差的影响。比如,如果使用具有随机测量误差的温度计测量温度,我们可以进行多次测量,然后求平均。因为误差是随机的,一些测量结果可能大于真值,其他结果可能低于真值。那么,估计可能就更接近真值。测量越多,那么估计可能就越接近真值。
另一方面,如果温度计是有偏差的,那么估计也具有恒定的系统误差。
本手册中的所有示例都假设是**无偏系统(unbiased systems)。
总结
下图展示了测量的统计信息:
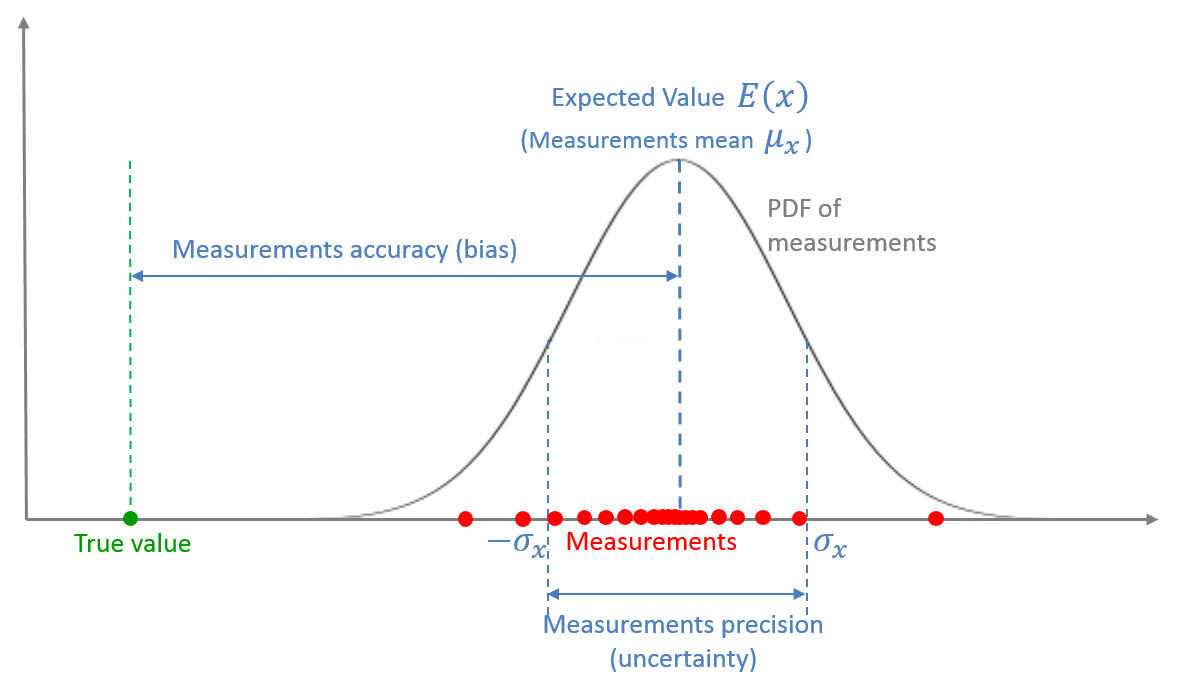
测量是随机变量,通过概率密度函数进行描述。随机变量的期望是测量的均值。测量均值和真值间的偏差是测量准确率,也称为偏差或系统测量误差。分布的分散程度表示测量的精度,也称为测量噪声或随机测量误差或测量不确定性。
参考链接
更新记录
2020.04.18 init

