这一节介绍了一维中的卡尔曼滤波。本节的目的是不使用那些复杂的数学工具,而是通过简单直观的方式解释卡尔曼滤波的概念。
我们将逐步介绍卡尔曼滤波方程:
- 首先,通过没有过程噪声的简单示例推导卡尔曼滤波方程
- 然后,通过有过程噪声的示例推导卡尔曼滤波方程
无过程干扰的一维卡尔曼滤波
之前提到过,卡尔曼滤波需要五个方程,已经给出了其中两个:
- 状态更新方程
- 动态模型方程
此节,我们将进一步推导另外三个卡尔曼滤波方程。
首先回忆一下第一个黄金测量的示例,我们进行了多次测量,并通过计算均值估计黄金的重量,得到了下图:
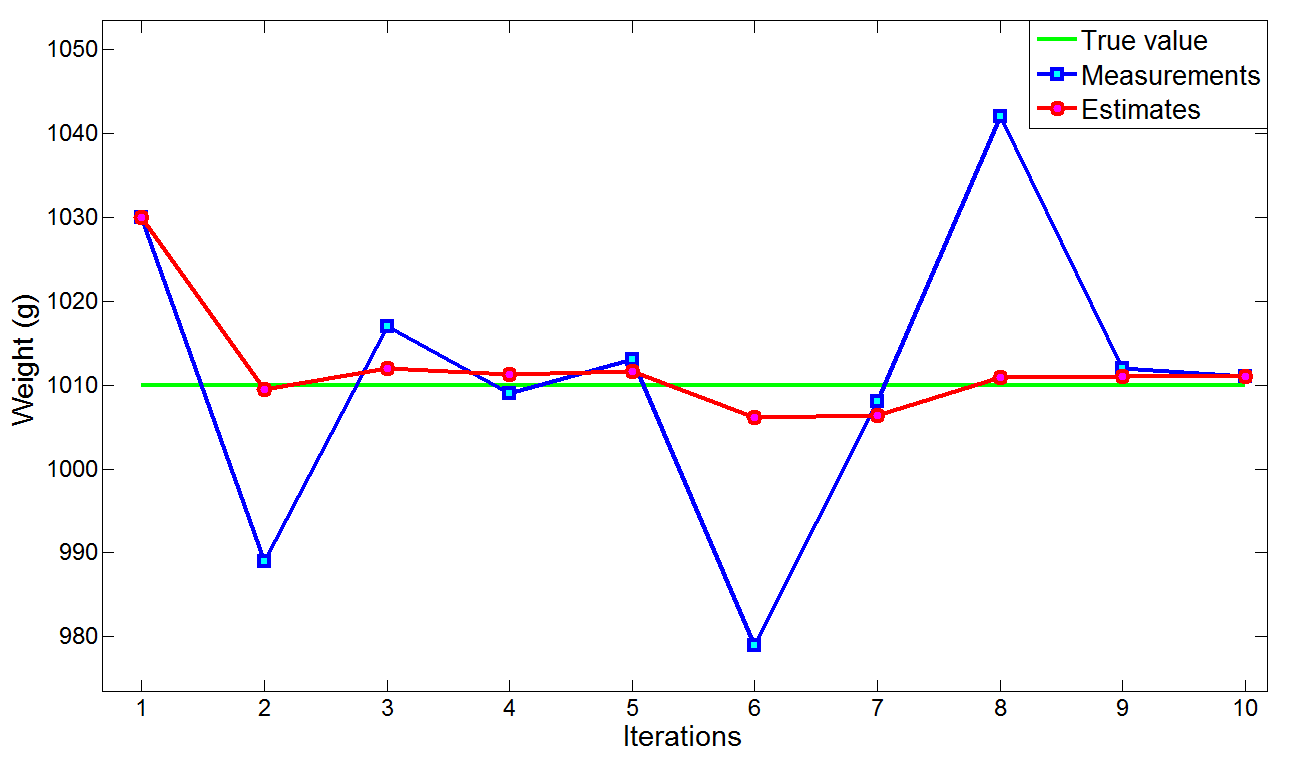
从上图中我们可以看出:真值、估计值和测量以及测量的次数。
测量和真值间的差称为测量误差(measurement errors)。因为测量误差是随机的,可以通过方差进行描述。测量误差可以由设备供应商提供,或者通过校准程序推测。 测量误差的方差通常称为测量不确定性(measurement uncertainty)。
注意:在一些文献中,测量的不确定性(measurement uncertainty)也称为测量误差(measurement error)。
我们将通过 $r$ 表示测量不确定性(measurement uncertainty)。
估计和真值间的差异称为估计误差(estimate error)。随着测量次数的增多,估计误差越来越小,不断向0收敛。即估计值不断向真值收敛。我们不知道估计误差是什么,但是我们可以估计估计中的不确定性。
我们通过 $p$ 表示估计不确定性(estimate uncertainty)。
首先,让我们看一下质量测量的概率密度函数(PDF (Probability Density Function))。
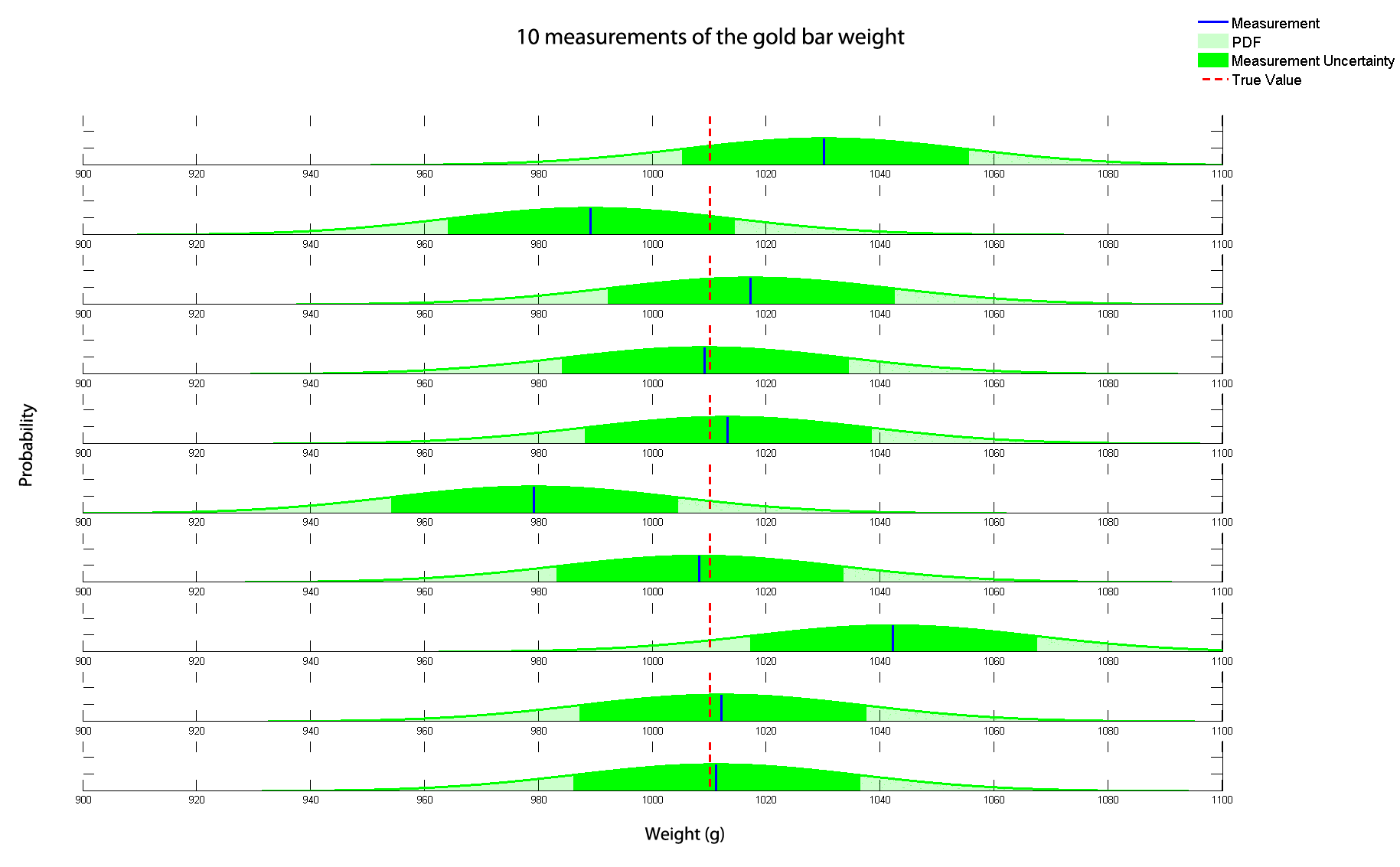
下图中展示了10次黄金质量的测量结果:
- 蓝色表示测量结果;
- 红色虚线表示真值;
- 绿色线表示测量的概率密度函数;
- 绿色区域表示测量的标准差,即68.26%的真值位于此区域的概率。
如图所示,10次测量中有8次的结果和真值非常接近。因此,真值在1个方差范围内。
测量的不确定性 $r$ 就是测量的方差 $\sigma^2$。
一维中的卡尔曼滤波方程
我们继续推导卡尔曼滤波方程中的第三个方程:卡尔曼增益方程。下面将给出一种直观的卡尔曼增益方程的直观推导。后面的章节将给出数学推导。
在KF中,$\alpha - \beta (-\gamma)$ 参数是在每次滤波迭代动态计算。这些参数称为卡尔曼增益(Kalman Gain),通过 $K_n$ 表示。
下面是卡尔曼增益方程:
$$
K_{n}=\frac{\text {Uncertainty in Estimate}}{\text {Uncertainty in Estimate} + \text {Uncertainty in Measurement }} =\frac{p_{n, n-1}}{p_{n, n-1}+r_{n}}
\
\
$$
其中 $p_{n, n-1}$ 是外推估计不确定性, $r_{n}$ 是测量不确定性。
卡尔曼增益的值在0到1之间。
$$ 0 \le K_n \le 1 $$
让我们重写状态方程:
$$ \hat{x}{n, n}=\hat{x}{n, n-1}+K_{n}\left(z_{n}-\hat{x}_{n, n-1}\right)=\left(1-K_{n}\right) \hat{x}_{n, n-1}+K_{n} z_{n} $$
卡尔曼增益 $K_n$ 表示给观测的权重,而 $(1 - K_n)$ 表示给估计的权重。
当测量的不确定性很大且估计的不确定性很小的时候,卡尔曼增益接近0。因此,估计的权重很大,而测量的权重则很小。
另一方面,当测量的不确定性很小且估计的不确定性很大时,卡尔曼增益接近1。因此,估计的权重很小,而测量的权重很大。
如果测量的不确定性等于估计的不确定性,那么卡尔曼增益为0.5。
卡尔曼增益的目的是,给定测量时,应该如何更改估计值,即赋予估计多大的权重。
卡尔曼增益方程是卡尔曼滤波的第三个方程。
更新一维中的估计的不确定性
下列方程定义了估计不确定性的更新方式:
$$ p_{n,n} = (1 - K_n) (p_{n, n-1}) $$
其中,$K_n$ 表示卡尔曼增益,$p_{n, n-1}$ 表示前一次滤波估计时计算的估计的不确定性,$p_n$ 表示当前状态估计的不确定性。
此方程更新的是当前状态的估计的不确定性,也称为协方差更新方程(Covariance Update Equation)。在之后的章节将解释为什么称为协方差。
从上述方程中可以明显看出:因为 $(1 - K_n) \le 1(1 - K_n) \le 1$ ,估计的不确定性随着每次滤波迭代在逐渐减小。当测量不确定性大时,卡尔曼增益将较小。因此,估计的不确定性的收敛将是缓慢的。然而,当测量的不确定性小时,卡尔曼增益较大,同时估计的不确定性将很快收敛到0。
协方差更新方程是卡尔曼滤波的第四个方程。
一维中的估计的不确定性外推
和状态外推类似,估计的不确定性外推是通过动态模型方程实现的。
在第二个示例中,一维雷达的位置追踪,预测目标的位置是:
$$
\begin{array}{c}
\hat{x}{n+1, n}=\hat{x}{n, n}+\Delta t \hat{\dot{x}}{n, n} \
\hat{\dot{x}}{n+1, n}=\hat{\dot{x}}_{n, n}
\end{array}
$$
即预测的位置等于当前的位置加上当前估计的速度和时间的乘积。预测的速度等于当前的速度估计(假设是常数速度模型)。
估计的不确定性外推是:
$$
\begin{array}{c}
p_{n+1, n}^{x}=p_{n, n}^{x}+\Delta t^{2} \cdot p_{n, n}^{v} \
p_{n+1, n}^{v}=p_{n, n}^{v}
\end{array}
$$
其中,$p^x$ 表示位置的估计不确定性,$p^v$ 表示速度的估计不确定性。
即,预测位置的不确定性等于当前位置的不确定性加上当前速度的不确定性估计和时间的平方的乘积。预测速度的不确定性等于当前速度估计的不确定性(假设是常数速度模型)。
如果你疑惑为什么是时间的平方,可以看一下方差期望的推导。
在第一个示例中,即黄金质量测量,动态系统是常数。因此,估计不确定性的外推是:
$$ p_{n+1,n} = p_{n, n} $$
其中,$p$ 表示黄金质量的估计的不确定性。
估计不确定性外推方程也称为协方差外推方程Covariance Extrapolation Equation),是卡尔曼滤波方程的第五个方程。
卡尔曼滤波方程组
这一节我们将上述所有部分放到一起。类似 $\alpha - \beta - (\gamma)$ 滤波,卡尔曼滤波利用了测量、更新、预测算法。
下图是关于卡尔曼滤波算法的简单示意图:
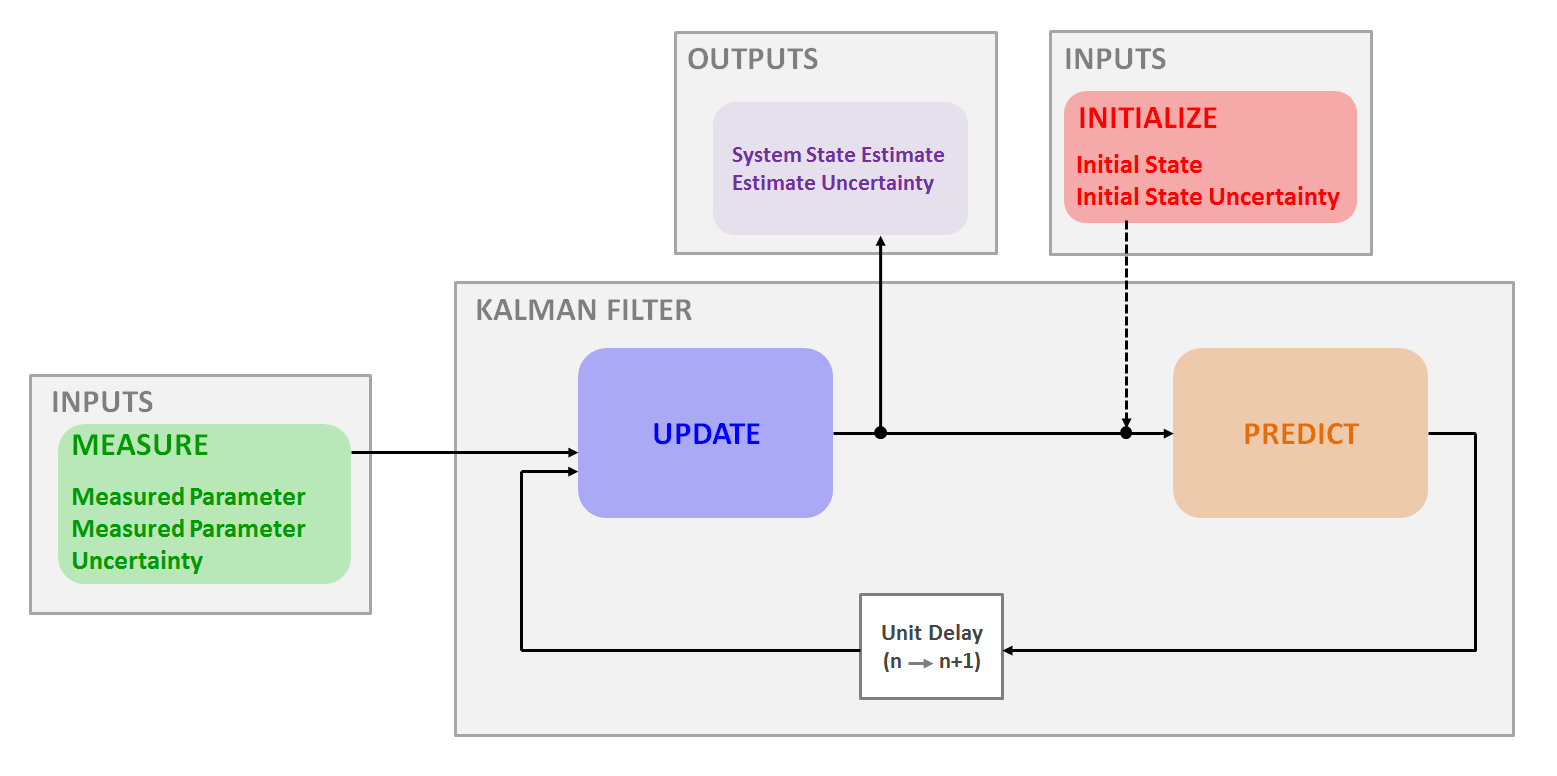
滤波输入
-
初始化
初始化仅执行一次,提供了两个参数:
- 初始系统状态 $\bar{x}_{1,0}$
- 初始状态不确定性 $p_{1, 0}$
初始参数可以由其他系统、其他过程或基于经验或理论的猜测。尽管初始猜测是不准确的,但是卡尔曼滤波仍能向真值收敛。
-
测量
测量是在每次滤波循环时进行,同样提供两个参数:
- 测量系统状态 $z_n$
- 测量不确定性 $r_n$
除了测量值外,卡尔曼滤波还需要测量的不确定性参数。通常,此参数由设备供应商提供,或者通过测量设备校准获取。雷达测量的不确定性依赖于几个参数:SNR (Signal to Nose Ratio), beam width, bandwidth, time on target, clock stability等。每个雷达都有不同的信噪比、波束宽度和到达目标的时间。因此,雷达将计算每次测量的不确定性,并报告给追踪者。
滤波输出
- 系统状态估计 $\hat{x}_{n ,n}$
- 估计的不确定性 $p_{n, n}$
除了系统状态估计外,卡尔曼滤波还提供估计的不确定性。之前提到过,估计的不确定性可通过下式计算:
$$ p_{n, n} = (1 - K_n) p_{n, n-1} $$
因为,$(1 - K_n) \le 1$,所以 $p_{n, n}$ 随着每次迭代逐渐减小。
因此,我们需要确定要使用多少观测。如果我们关注建筑的高度,那么我们可能需要关注方差为3 cm的测量精度。我们需要持续测量,直到**估计的不确定性(Estimation Uncertainty) ** $\sigma^2$ 小于 9 cm。
下表是对卡尔曼滤波方程组五个方程的总结:
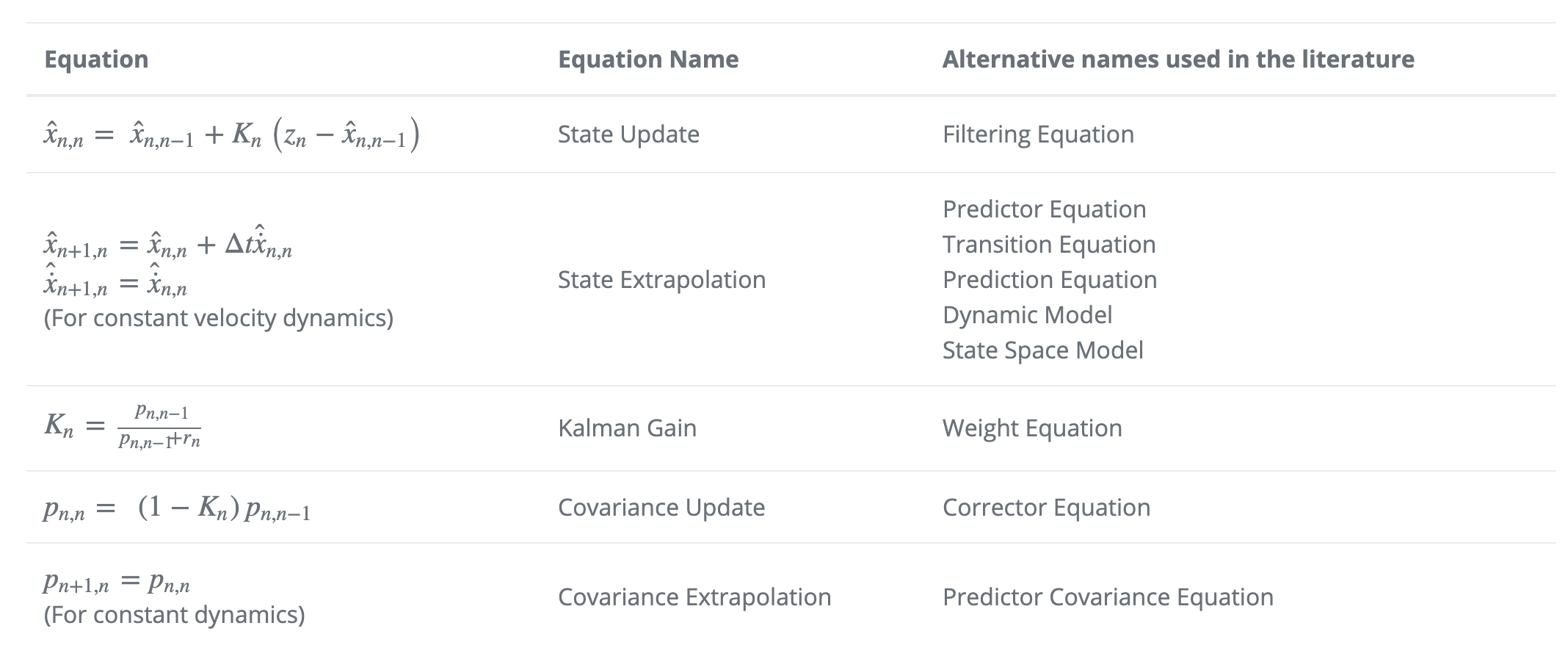
注意:状态外推方程和协方差外推方程依赖于动态系统。
上表展示了针对特定情况的卡尔曼滤波器方程的特殊形式。该方程式的一般形式将在稍后以矩阵符号的形式呈现。目前,我们的目标是了解卡尔曼滤波器的概念。
下图是卡尔曼滤波算法的详细示意图:
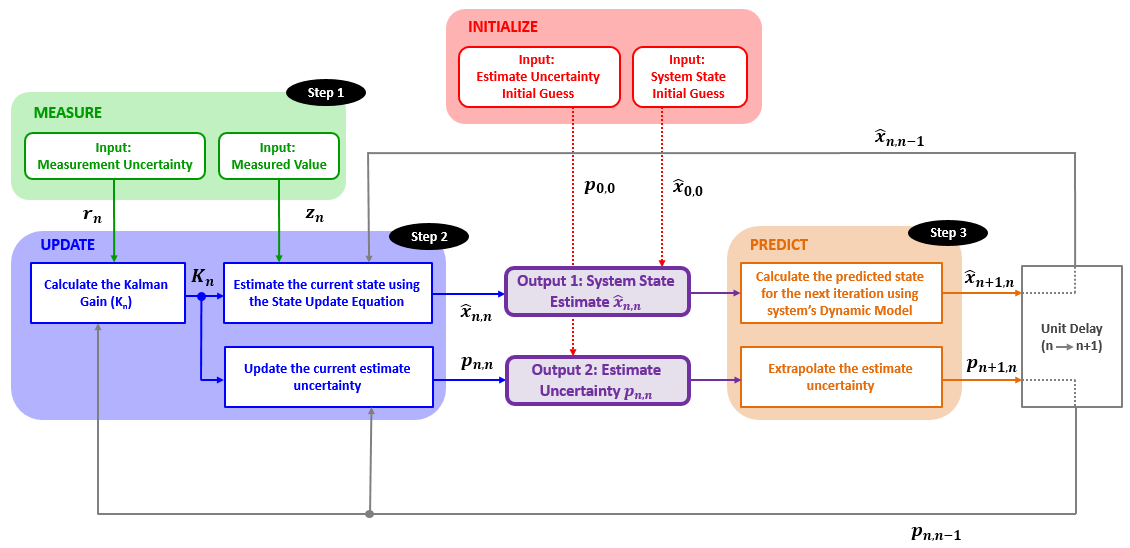
-
Step0 :初始化
如上所述,初始化仅执行一次,提供两个参数:
- 初始系统状态 $\hat{x}_{1,0}$
- 初始状态不确定性 $p_{1, 0}$
初始化后进行预测。
-
Step1 :测量
测量提供两个参数:
- 测量系统状态 $z_n$
- 测量不确定性 $r_n$
-
Step2 :状态更新
状态更新是对当前系统状态的估计。
状态更新处理输入是:
- 测量值 $z_{1, 0}$
- 测量不确定性 $r_n$
- 之前系统状态估计 $\hat{x}_{n, n-1}$
- 估计不确定性 $p_{n, n-1}$
基于上述输入,状态更新计算卡尔曼增益并输出两个参数:
- 当前系统状态估计 $\hat{x}_{n, n}$
- 当前状态估计的不确定性 $p_{n, n}$
这些参数就是卡尔曼滤波的输出。
-
Step3:预测
预测过程是基于系统动态模型对当前系统状态的外推,以及当前系统状态外推到新的状态的估计的不确定性。
-
At the first filter iteration the initialization outputs are treated as the Previous State Estimate and Uncertainty.
-
On the next filter iterations, the prediction outputs become the Previous State Estimate and Uncertainty.
-
在第一次滤波迭代时,初始化的输出被认为是之前的状态估计和估计的不确定性。注:是因为初始化后直接进行下一次状态的预测,这时候,初始化输入后经过系统状态估计和不确定性估计后的输出用于预测。所以初始化的输出会被当成是之前的状态估计和估计的不确定性。
-
在下一次滤波迭代,预测输出是之前状态估计和估计的不确定性。
卡尔曼增益
卡尔曼增益定义为当执行新的估计时,之前估计的权重和测量的权重。
高卡尔曼增益
相对于估计不确定性而言,低的测量不确定性将导致高的卡尔曼增益(接近1)。因此,新的估计将接近测量值。下图解释了在飞机追踪示例中,高卡尔曼增益对估计的影响。
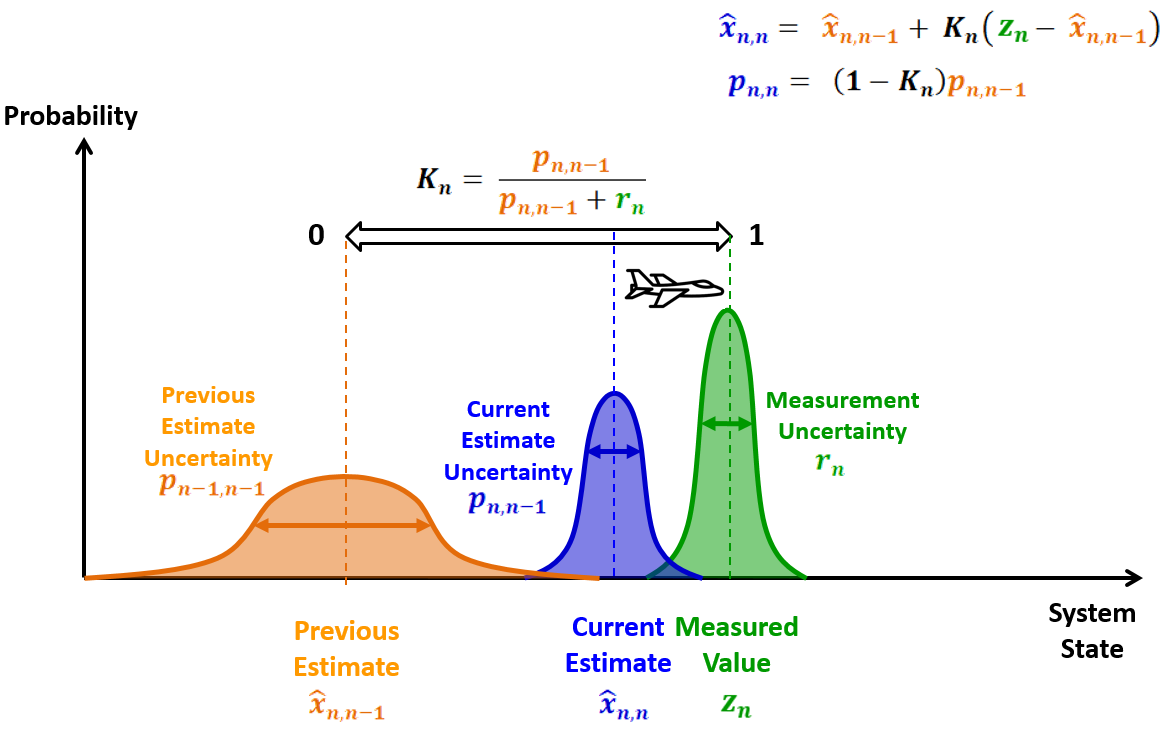
低卡尔曼增益
相对于估计不确定性而言,高的测量不确定性会导致低的卡尔曼增益(接近0)。因此,新的估计将接近之前的估计。下图解释了在飞机追踪示例中,低卡尔曼增益对估计的影响。

现在,我们理解了卡尔曼滤波算法,下面将针对数值示例进一步增强理解。
注意:如果你对卡尔曼增益的数学推导感兴趣,可以看一下一维卡尔曼增益推导。
示例五:估计建筑高度
假设我们使用非常不准确的测高仪测量建筑的高度,已知短时间内建筑的高度不随时间而变化。

数值计算
- 建筑的真实高度为 50 m;
- 测高仪的测量误差(标注差)是5 m;
- 10次的测量结果分别是:48.54m, 47.11m, 55.01m, 55.15m, 49.89m, 40.85m, 46.72m, 50.05m, 51.27m, 49.95m。
第0次迭代
初始化
可以通过目测估计建筑的高度:
$$ \hat{x}_{0, 0} = 60 m $$
现在我们初始化估计的不确定性。人类的估计误差(方差)大约是15 m。即 $\sigma = 15 m$。因此,方差是 $\sigma^2 = 225$。
$$ p_{0, 0} = 225 $$
预测
现在,我们根据初始化的值预测下一状态。因为建筑的高度短时间内不会随时间变化,系统动态是恒定的。
$$ \hat{x}{1, 0} = \hat{x}{0, 0} = 60 m $$
外推的估计不确定性(方差)也是恒定的:
$$ p_{1, 0} = p_{0, 0} = 225 $$
第一次迭代
Step1:测量
首次测量结果是:$z_1 = 48.54 m$
因为测高仪的测量误差的标准差是 5,方差是 25。因此,测量的不确定性是 $r_1 = 25$。
Step2:更新
计算卡尔曼增益
$$ K_1 = \frac{p_{1, 0}}{p_{1, 0} + r_1} = \frac{225}{225+25} = 0.9 $$
估计当前状态
$$ \hat{x}{1,1}=\hat{x}{1,0}+K_{1}\left(z_{1}-\hat{x}_{1,0}\right)=60+0.9(48.54-60)=49.69 m $$
更新当前状态估计的不确定性
$$ p_{1,1}=\left(1-K_{1}\right) p_{1,0}=(1-0.9) 225=22.5 $$
Step3 预测
因为系统的动态是恒定的,即建筑的高度不随时间变化。
$$ \hat{x}{2, 1} = \hat{x}{1, 1} = 49.69 m $$
外推的估计不确定性(方差)也不会发生变化:
$$ p_{2, 1} = p_{1, 1} = 22.5 $$
第二次迭代
单位时间延迟后,前一次迭代的预测估计成为当前迭代的前一次估计:
$$ \hat{x}_{2, 1} = 49.69 m $$
外推估计的不确定性等于前一次的估计不确定性
$$ p_{2, 1} = 22.5 $$
Step1 测量
第二次测量是:$z_2 = 47.11 m$
测量的不确定性是 $r_2 = 25$
Step2 更新
计算卡尔曼增益
$$ K_{2}=\frac{p_{2,1}}{p_{2,1}+r_{2}}=\frac{22.5}{22.5+25}=0.47 $$
估计当前状态
$$ \hat{x}{2,2}=\hat{x}{2,1}+K_{2}\left(z_{2}-x_{2,1}\right)=49.69+0.47(47.11-49.69)=48.47 m $$
更新当前状态不确定性
$$ p_{2,2}=\left(1-K_{2}\right) p_{2,1}=(1-0.47) 22.5=11.84 $$
Step3 预测
因为建筑的高度不随时间变化,因此,建筑高度等于:
$$ \hat{x}{3,2} = \hat{x}{2, 2} = 48.47 m $$
外推估计不确定性(方差)也不会发生变化:
$$ p_{3,2} = p_{2,2} = 11.84 $$
第3-10次的迭代结果省略。
下图是真值、测量和估计:
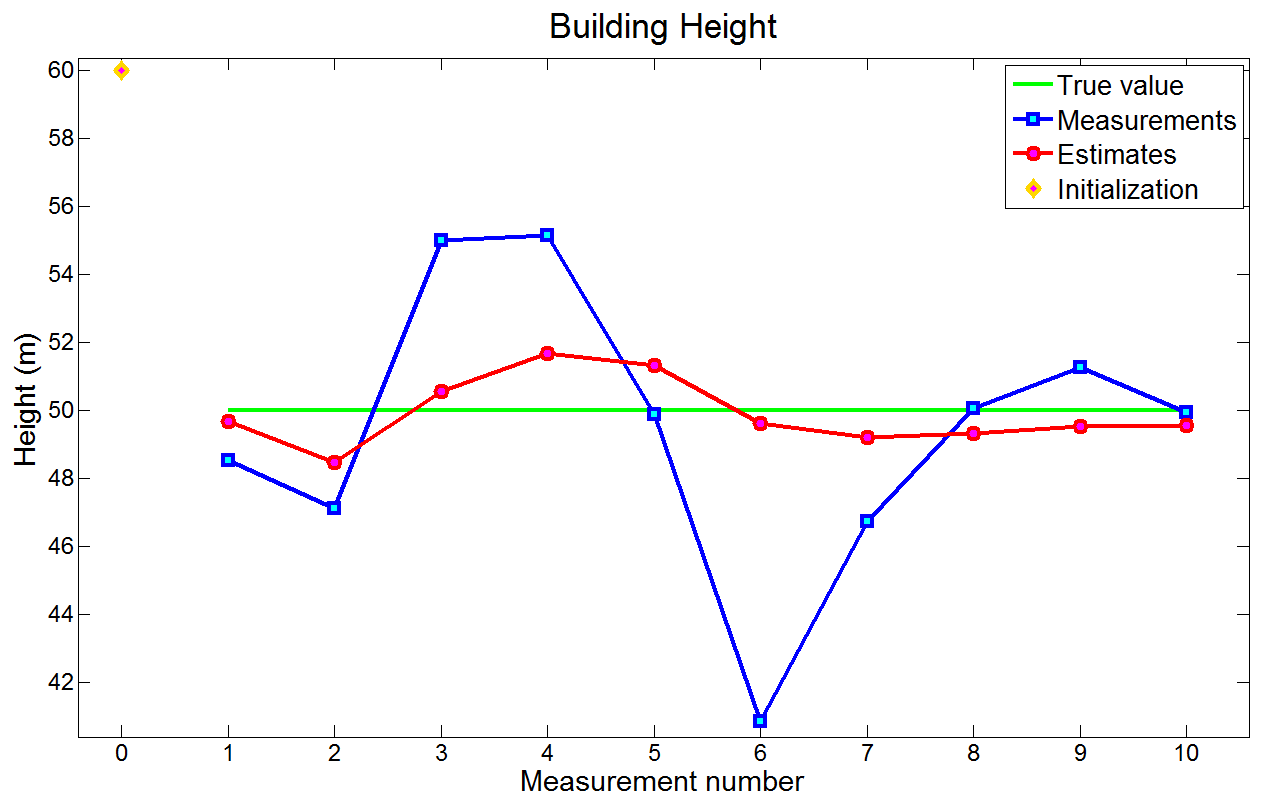
在7次测量之后,真值逐渐收敛到49.5 m。
下图是估计的不确定性和测量的不确定性
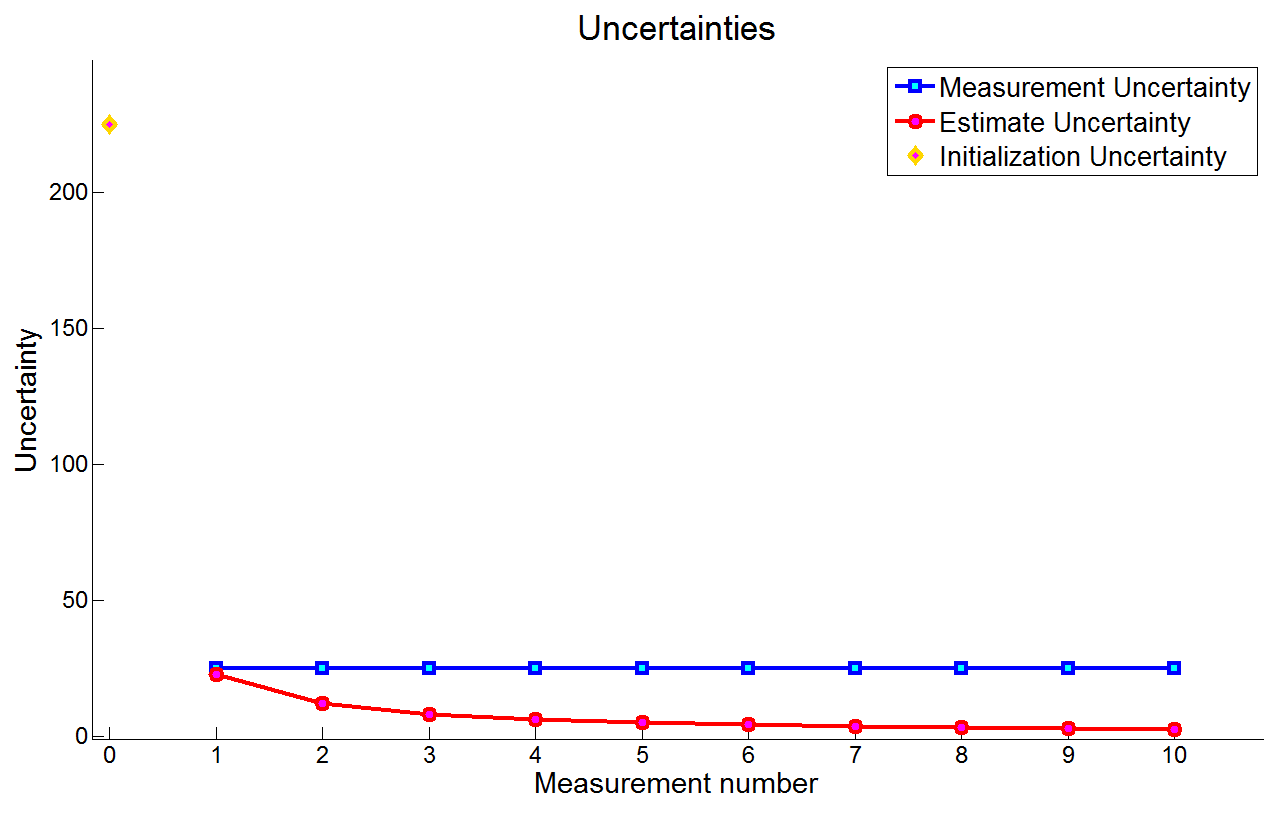
第一次滤波迭代时,估计不确定性和测量不确定性很接近,然后快速下降。10次测量之后,估计不确定性($\sigma^2$)为2.47,即估计误差标准差为 $\sigma = \sqrt{2.47} = 1.57 m$。
因此,可以认为建筑高度是:$49.57 m \pm 1.57 m$。
下图展示的是卡尔曼增益
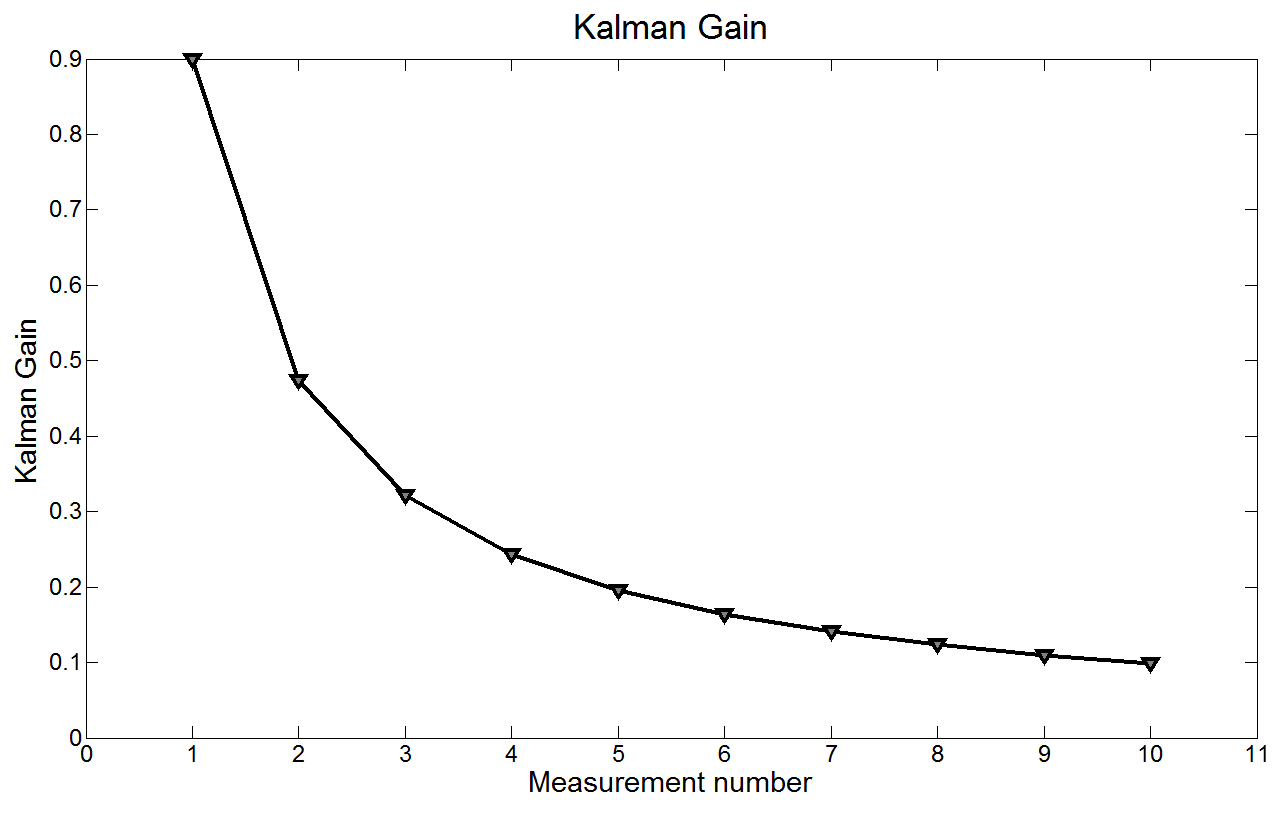
由图可知,卡尔曼增益不断降低,测量权重越来越小。
示例总结
此例中,我们使用一维卡尔曼滤波测量建筑高度。与 $\alpha - \beta - (\gamma)$ 滤波不同的是,卡尔曼增益是动态的,而且依赖于测量设备的精度。
起初,卡尔曼增益初始时并不准确。因此,在状态更新方程中,测量的权重很大,估计不确定性很高。
随着每一次迭代的进行,测量权重越来越小,估计不确定性也越来越小。
卡尔曼滤波的输出包括估计和估计的不确定性。
一维卡尔曼滤波完整模型
下面,我们更新有过程噪声的协方差外推方程。
过程噪声
真实世界中,动态模型总是具有不确定性。例如,想要估计电阻器的阻抗时,我们假设属于恒定模型,即电阻不随测量而变化。然而,电阻会因环境温度的不同发生轻微的变化。当用雷达跟踪弹道导弹时,动力学模型的不确定性包括目标加速度的随机变化。对于飞机而言,由于飞机的操纵,不确定性要大得多。
另一方面,当我们使用GPS接收器估算静态物体的位置时,由于静态物体不会移动,因此动态模型的不确定性为零。动态模型的不确定性称为过程噪声。在文献中,它也称为工厂噪声,行驶噪声,动力学噪声,模型噪声和系统噪声。过程噪声产生估计误差。
之前的示例中,我们估计了建筑的高度,由于建筑的高度是固定的,我们没有考虑过程噪声。
过程噪声方差 用 $q$ 表示。协方差外推方程 应包括 过程噪声方差。
对于恒定动态系统而言,协方差外推方程为:
$$ p_{n+1,n} = p_{n,n} + q_n $$
下面是一维中的更新卡尔曼滤波方程:
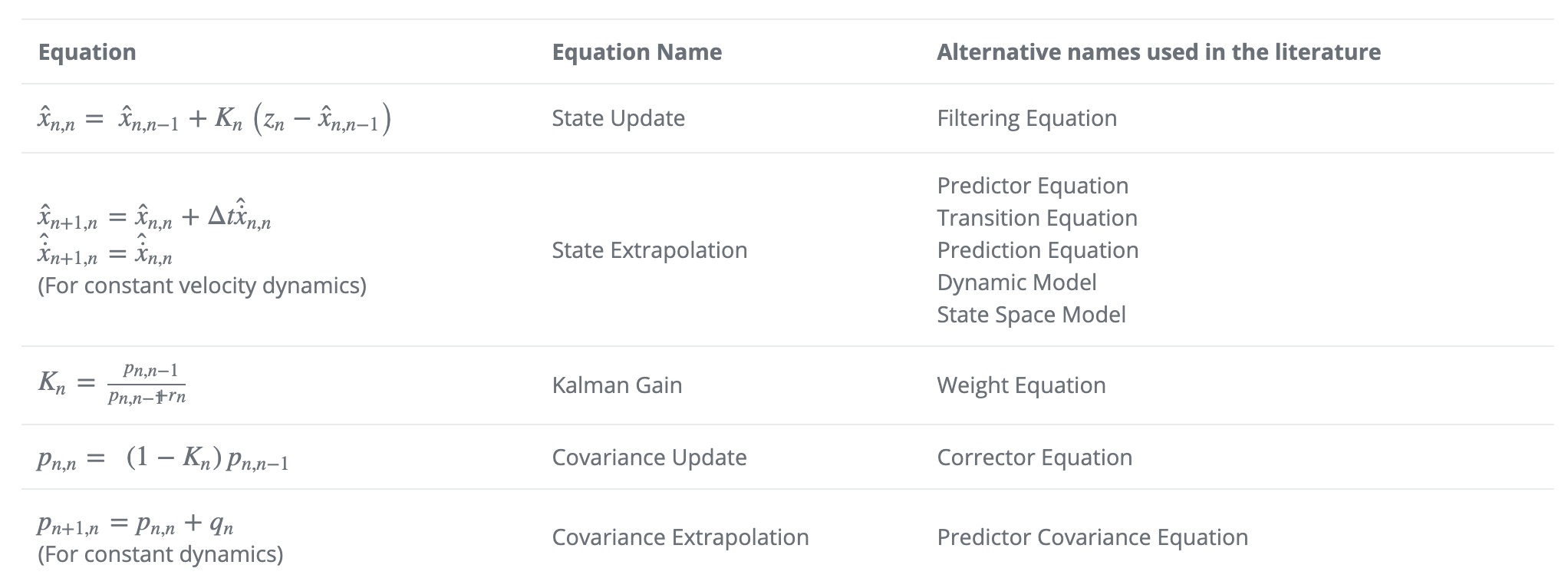
注意:状态外推方程和协方差外推方程依赖于系统动态。
注意:上表演示了针对特定情况量身定制的卡尔曼滤波器方程的特殊形式。该方程式的一般形式将在稍后以矩阵符号的形式呈现。目前,我们的目标是了解卡尔曼滤波器的概念。
示例6 估计容器中液体温度
下面,我们将估计容器中液体的温度。

我们假设在稳定状态下,液体的温度是常数。然而,真实的液体温度可能存在波动。我们可以通过如下方程描述动态系统:
$$ x_n = T + w_n $$ 其中,$T$ 是常数温度,$w_n$ 是方差为 $q$ 的随机过程噪声。
数值计算示例
- 首先,假设真实温度为 50 摄氏度;
- 假设我们 有一个精确的模型,然后假设过程噪声方差($q$)为 0.0001;
- 测量误差(标准差)是 0.1 摄氏度;
- 每5 s测量一次;
- 每次测量时的真实温度为:49.979 , 50.025, 50, 50.003, 49.994, 50.002, 49.999, 50.006, 49.998, 49.991;
- 10次测量结果为:49.95, 49.967, 50.1, 50.106, 49.992, 49.819, 49.933, 50.007, 50.023, 49.99。
下图是真实温度和测量结果的对比:
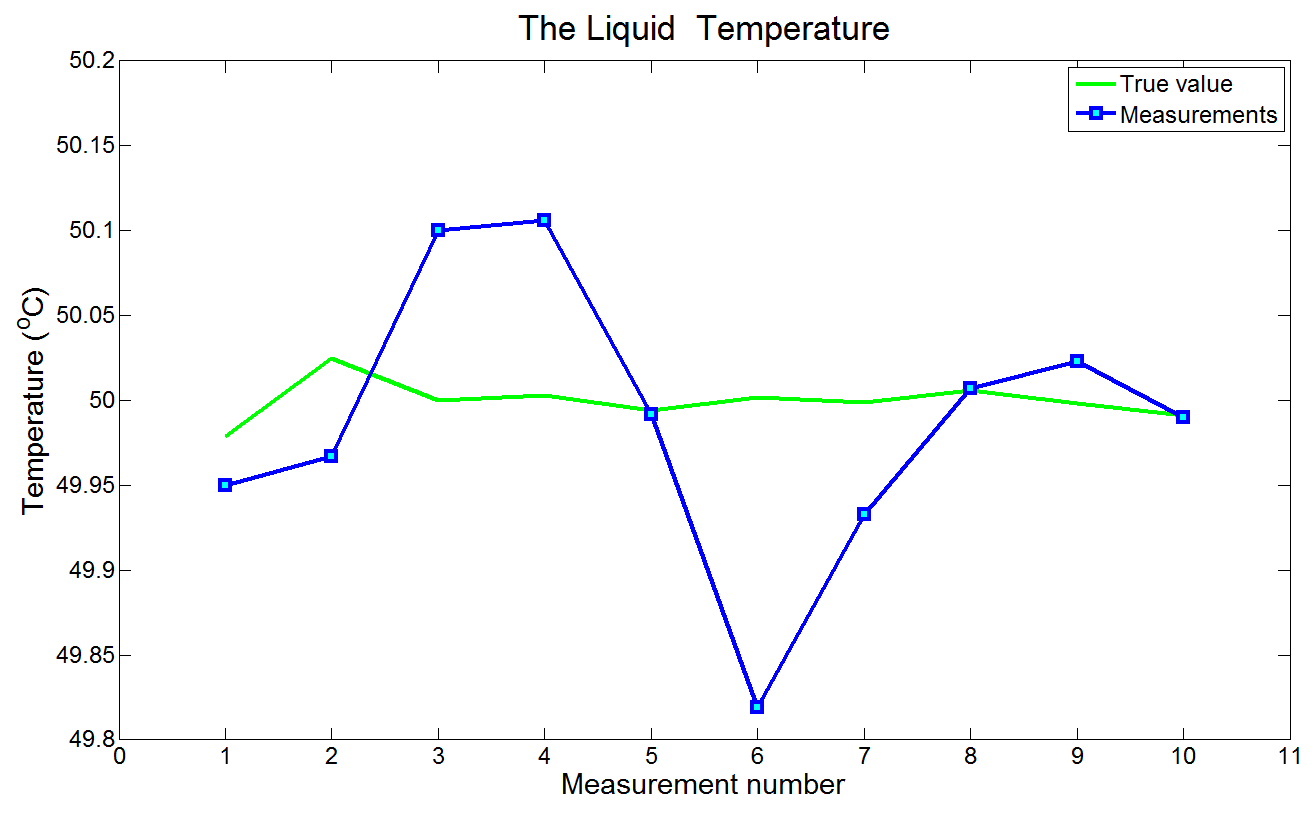
第0次迭代
在第一次迭代前,我们必须初始化卡尔曼滤波并预测下一次状态(第一次的状态)。
初始化
我们不知道液体的温度,首先给出一个猜测值:
$$ \hat{x}_{0, 0} = 10^\circ C $$
我们的猜测偏差很大,首先设置初始估计误差 $\sigma$ 为100。初始化的估计不确定性 是误差方差 ($\sigma^2$)。
$$ p_{0, 0} = 100^2 = 10000 $$
初始化的方差非常大,如果我们使用了更精确的值初始化,卡尔曼滤波将更快收敛。
预测
现在,我们基于初始化的值预测下一次状态。
因为我们的模型是常数模型,预测估计等于当前的状态。
$$ \hat{x}_{1, 0} = 10^\circ C $$
外推估计不确定性(方差)是
$$ p_{1, 0} = p_{0, 0} + q = 10000 + 0.0001 = 10000.0001 $$
第一次迭代
Step1 测量
测量值为 $z_1 = 49.95^\circ C$
因为测量误差($\sigma$)是0.1,方差($\sigma^2$)是0.01。因此,测量不确定性是 $r_1 = 0.01$
Step2 更新
计算卡尔曼增益
$$ K_1 = \frac{p_{1,0}}{p_{1,0}+r_1} = \frac{10000.0001}{10000.0001+0.01} = 0.999999 $$
卡尔曼增益接近1,表明我们的估计误差远远大于测量误差。因此,估计权重被忽略,测量权重接近1。
估计当前状态:
$$ \hat{x}{1,1}=\hat{x}{1,0}+K_{1}\left(z_{1}-\hat{x}_{1,0}\right)=10+0.999999(49.95-10)=49.95^{\circ} \mathrm{C} $$
更新当前估计不确定性
$$ p_{1,1}=\left(1-K_{1}\right) p_{1,0}=(1-0.999999) 10000.0001=0.01 $$
Step3 预测
因为动态系统是恒定的,即液体温度不随时间变化,则
$$ \hat{x}{2,1} = \hat{x}{1,1} = 49.95^\circ C $$
外推估计不确定性(方差)是:
$$ p_{2,1} = p_{1,1} + q = 0.01+0.0001=0.0101 $$
第2到10次迭代过程省略。
下图是真值、测量值和估计值的情况:可以看到估计值逐渐向真值收敛。
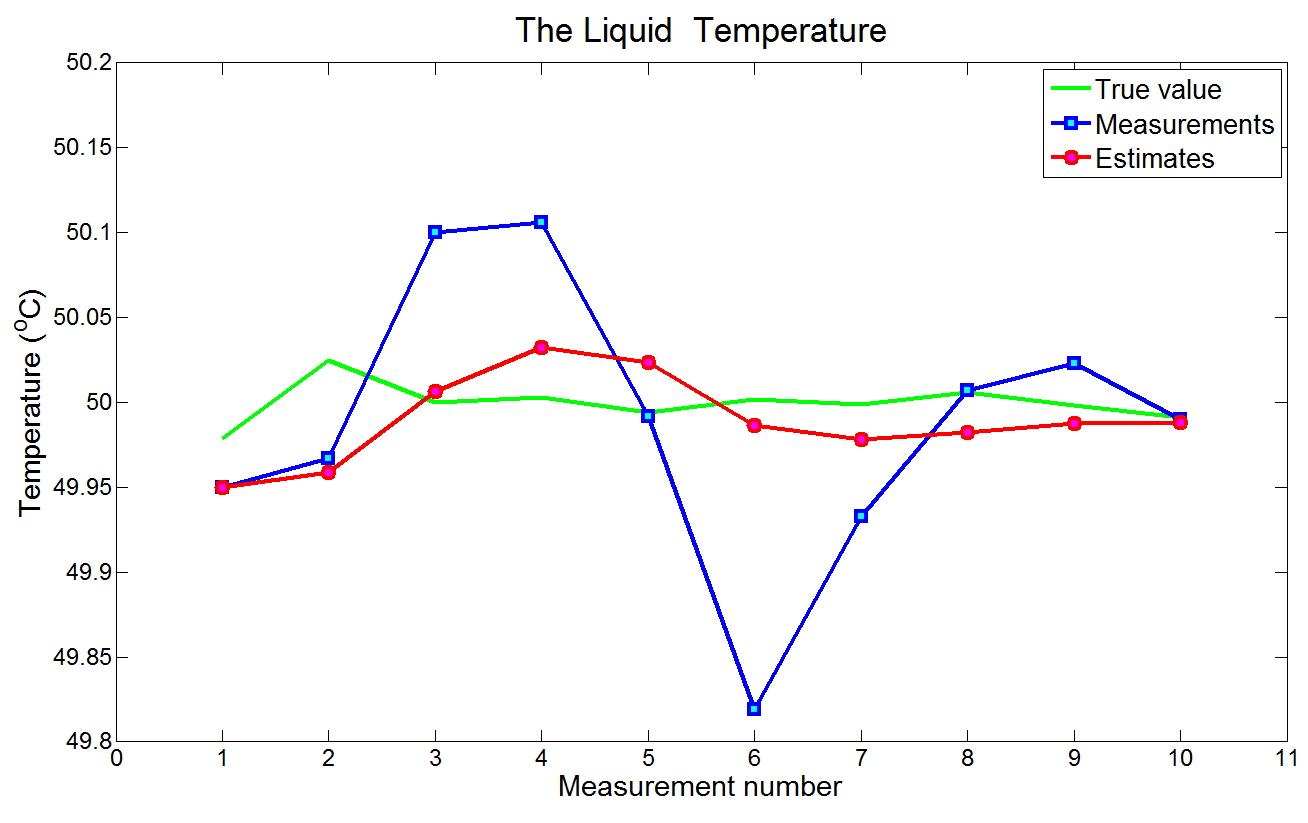
下图展示的是估计误差:
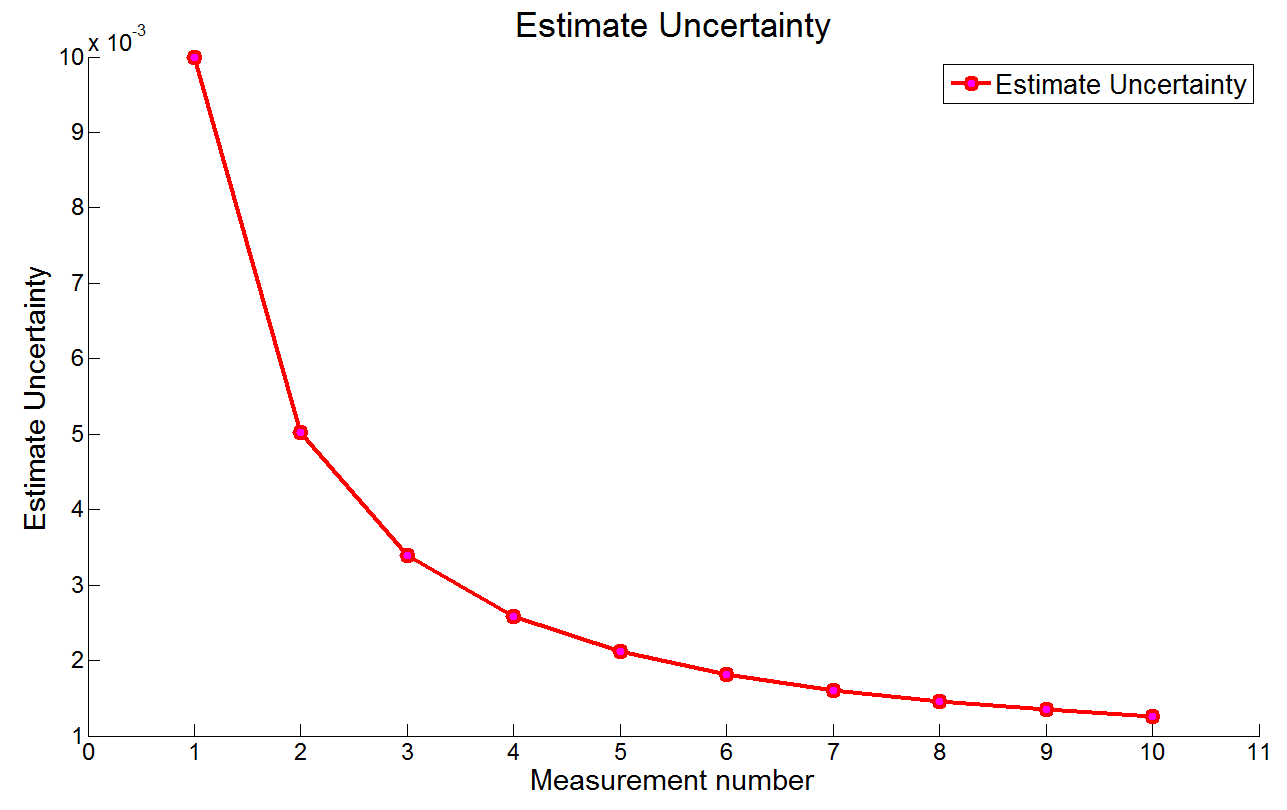
估计不确定性迅速下降。10次测量之后,估计不确定性是0.0013。估计误差的标准差为:$\sigma = \sqrt(0.0013) = 0.036^\circ C$。
因此,可以说液体的估计温度是:$49.988 \pm 0.036^\circ C$。
下图展示的是卡尔曼增益:
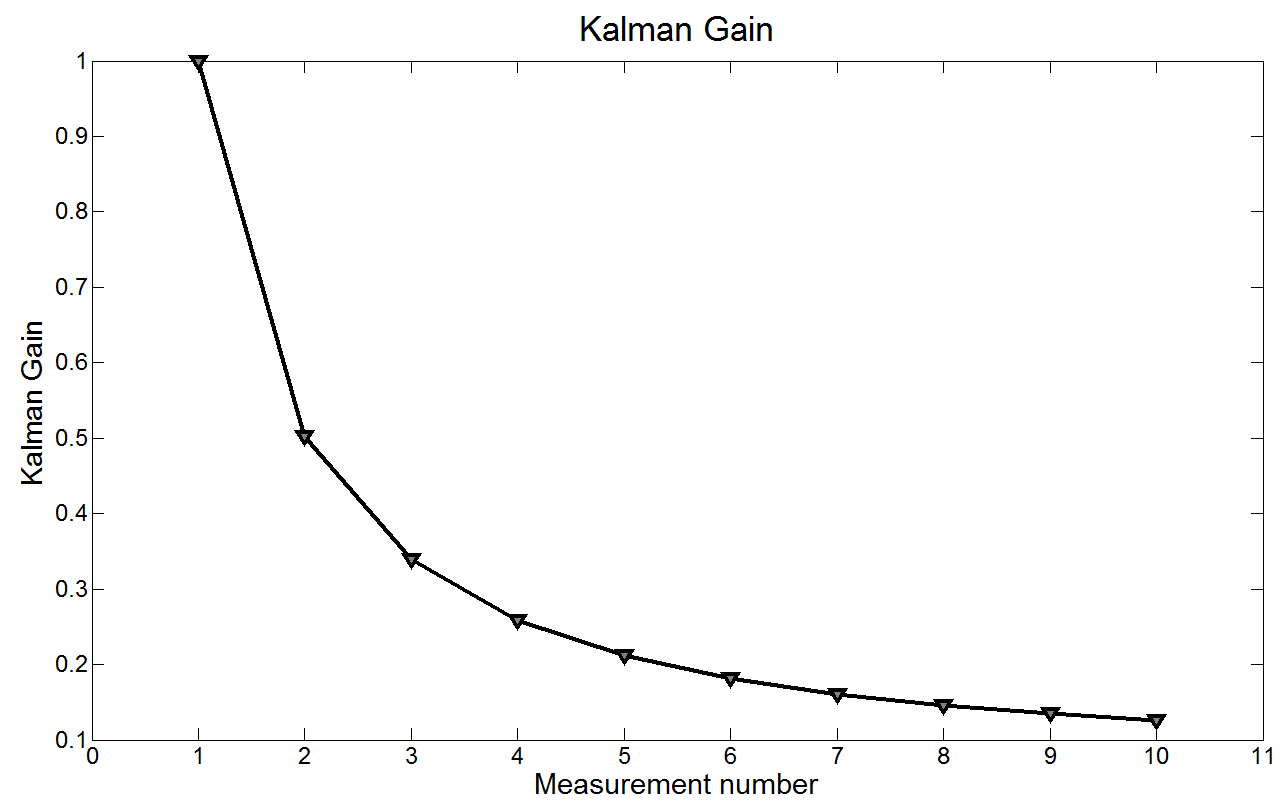
如图所示,卡尔曼增益逐渐降低,测量权重越来越小。
示例总结
此例中,我们使用一维卡尔曼滤波测量了液体温度。机关系统动态包括了随机过程噪声,但卡尔曼滤波仍提供了较好的估计结果。
示例7 估计加热液体的温度
类似之前的示例,此例中我们继续估计容器中液体的温度。只是动态系统不再是恒定的,液体将以每秒 $0.1^\circ C$ 的速率进行加热。
卡尔曼滤波参数类似之前的例子:
- 假设我们 有一个精确的模型,然后假设过程噪声方差($q$)为 0.0001;
- 测量误差(标准差)是 0.1 摄氏度;
- 每5 s测量一次;
- 动态系统是恒定的:即使真实情况不是恒定的,但此处我们仍将系统当成恒定不变的,即温度不会随时间发生变化;
- 每次测量对应的真实温度为:50.479, 51.025, 51.5, 52.003, 52.494, 53.002, 53.499, 54.006, 54.498, 54.991;
- 10次测量结果为:50.45, 50.967, 51.6o, 52.106, 52.492, 52.819, 53.433, 54.007, 54.523, 54.99。
下图是10次测量结果和对应的真值:
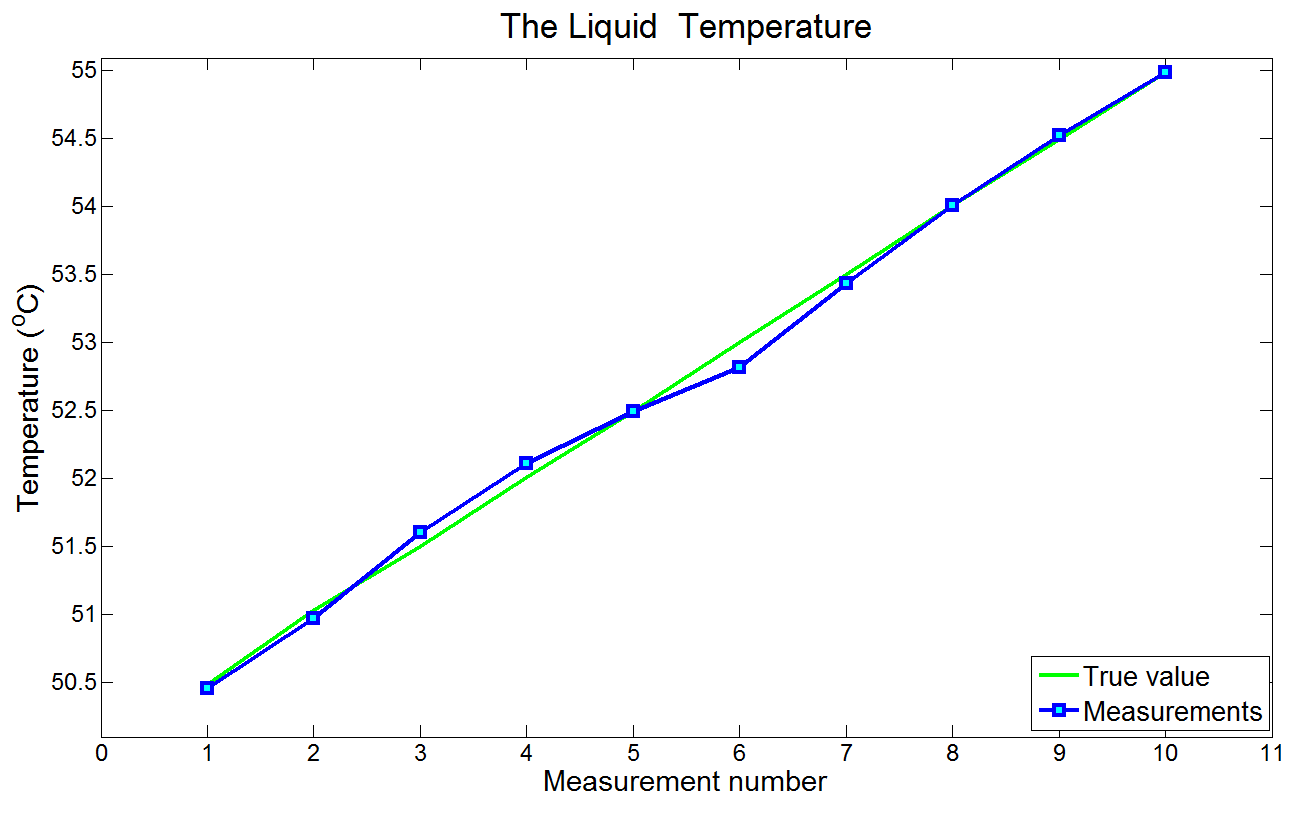
第0次迭代
与之前的示例类似,在第一次迭代之前,必须要初始化卡尔曼滤波并进行下一次预测:
初始化
首先还是猜测温度值:$\hat{x}{0,0} = 10^\circ C$。我们的猜测误差很大,所以我们设置初始估计误差($\sigma$)为 100,初始化的估计不确定性是误差方差($\sigma^2$):$p{0,0} = 100^2 = 10000$。
初始化的方差很大。如果使用更合适的值进行初始化,那么卡尔曼滤波将更快收敛。
预测
现在,我们基于初始化的值预测下一状态。因为我们的模型是常数动态模型,预测估计等于当前的估计:$\hat{x}{1,0} = 10^\circ C$。外推估计误差(方差)为:$p{1,0} = p_{0,0} + q = 100^2 + 0.0001 = 10000.0001$。
第1到10次的迭代结果省略。
下图是真值、估计值和测量值的对比结果。

如果所示,卡尔曼滤波没有提供准确的估计。这是因为在卡尔曼滤波中出现了滞后误差(lag error)。我们在示例3中也碰到了滞后误差,我们当时使用了匀速的飞机速度的 $\alpha - \beta$ 滤波估计具有加速度的飞机的位置。在示例4中,我们通过使用具有加速度的 $\alpha - \beta - \gamma$ 滤波代替 $\alpha - \beta$ 滤波消除了滞后误差的影响。
在卡尔曼滤波中导致滞后误差的原因是:
- 动态模型没能很好的拟合示例;
- 过程模型的可靠性。我们选择了比较低的过程噪声(q = 0.0001),然而真实的温度波动更大。
注意:滞后误差应该是常数。因此,估计曲线应与真实值曲线具有相同的斜率。上图仅显示了10个初始测量值,不足以收敛。下图显示了前100次测量的恒定滞后误差。
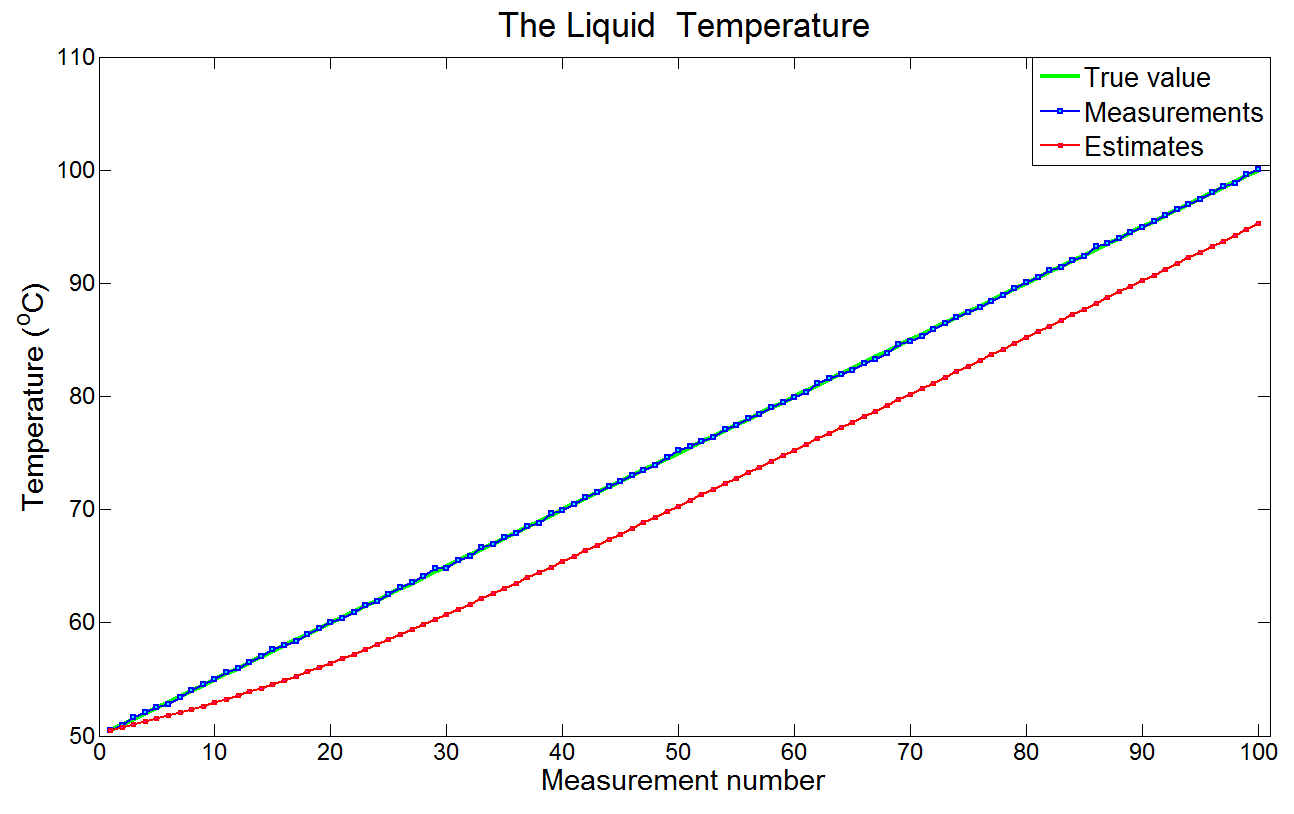
可以通过如下两种方法消除滞后误差:
- 如果我们知道液体的温度是线性变化的,我们可以定义新的模型,考虑液体温度的线性变化。在示例4中采用的是此方法。但是,如果温度的变化不能建模,那么此方法就不能改善卡尔曼滤波的性能;
- 另一方面,因为我们的模型不能很好的定义,可以通过增加过程噪声($q$)调整过程模型的可靠性。详细信息可以参考示例8。
示例总结
此示例中,我们使用常数动态模型的一维卡尔曼滤波测量了加热液体的温度。在卡尔曼滤波的估计中,我们观测到了滞后误差。滞后误差是由于错误的动态模型定义和错误的过程模型定义所导致。可以通过调整动态模型或过程模型的定义处理滞后误差。
示例8 估计加热液体的温度
此示例与示例7类似。只是在此示例中,因为不能很好的定义模型,我们将过程不确定性$q$ 从0.0001增加到0.15。
第0次迭代
与之前的示例类似,在第一次迭代之前,必须要初始化卡尔曼滤波并进行下一次预测:
初始化
首先还是猜测温度值:$\hat{x}{0,0} = 10^\circ C$。我们的猜测误差很大,所以我们设置初始估计误差($\sigma$)为 100,初始化的估计不确定性是误差方差($\sigma^2$):$p{0,0} = 100^2 = 10000$。
初始化的方差很大。如果使用更合适的值进行初始化,那么卡尔曼滤波将更快收敛。
预测
现在,我们基于初始化的值预测下一状态。因为我们的模型是常数动态模型,预测估计等于当前的估计:$\hat{x}{1,0} = 10^\circ C$。外推估计误差(方差)为:$p{1,0} = p_{0,0} + q = 100^2 + 0.15 = 10000.15$。
第1到10次的迭代结果省略。
下图是真值、测量值和估计值。
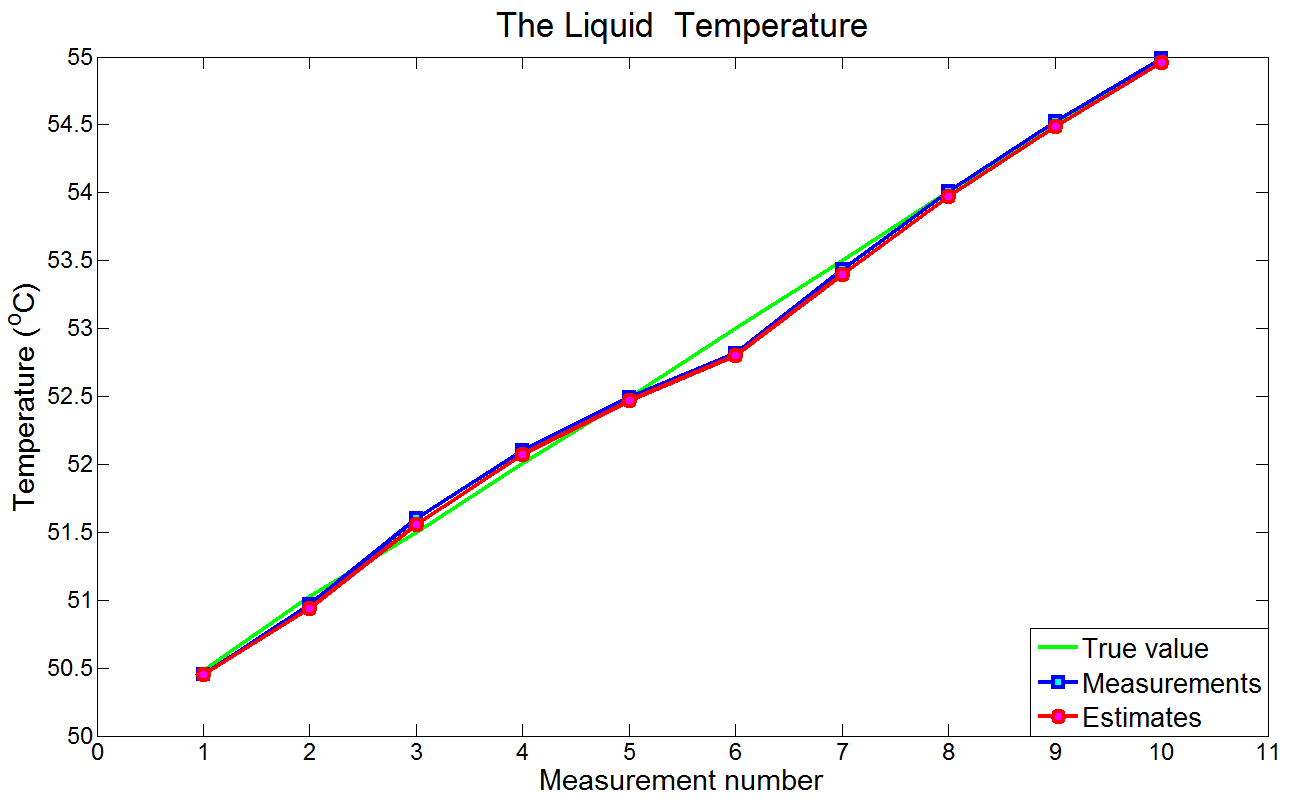
如上图所示,估计值和测量值很接近,没有出现滞后误差。
下图展示的是卡尔曼增益:
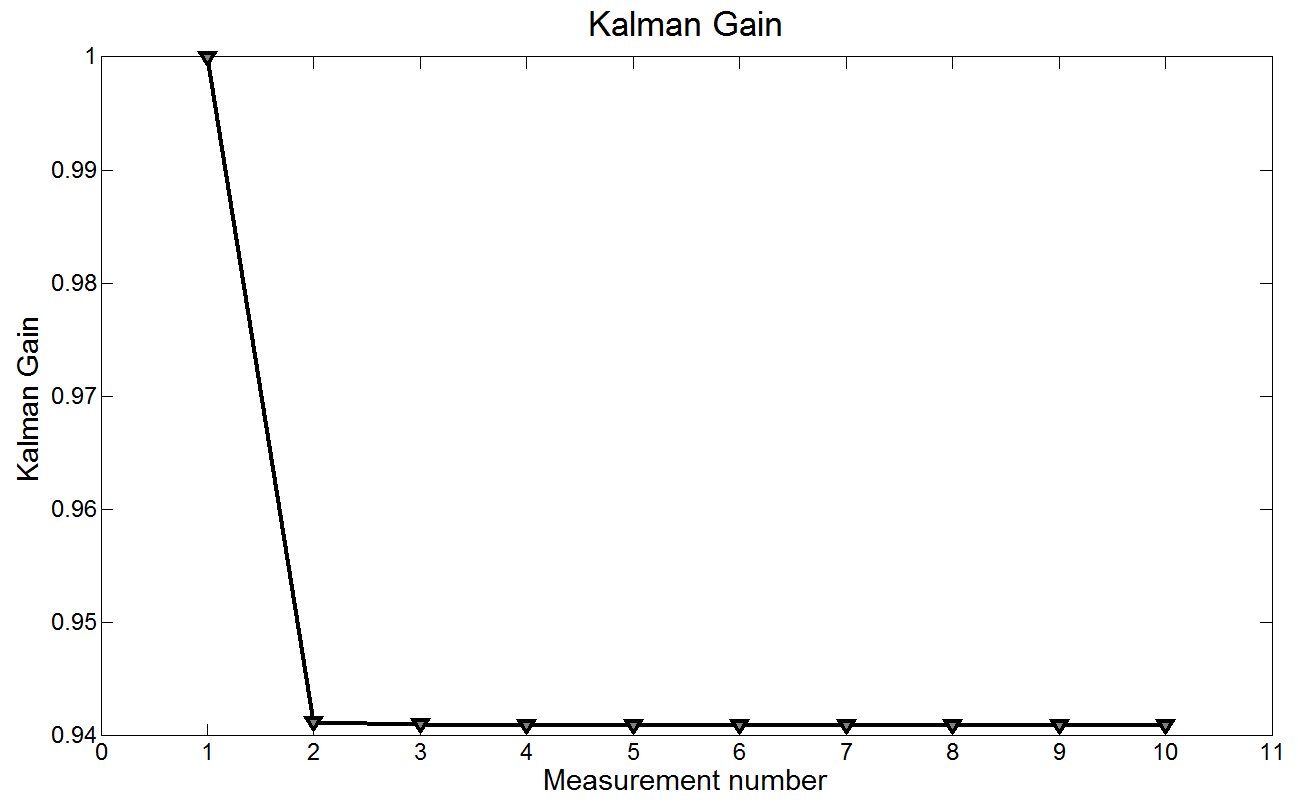
由于存在很大的过程不确定性,测量的权重大于估计的权重。因此,卡尔曼增益更高,收敛在0.94。
示例总结
我们可以通过设置较高的过程不确定性值避免滞后误差。然而,因为我们不能很好的定义模型,我们得到的噪声估计很可能等于测量,而且我们忽略了卡尔曼滤波的目标。
最佳的卡尔曼滤波器实施方案应包括非常接近实际的模型,并为过程噪声留出很小的空间。但是,精确模型并不总是可用,例如,飞机驾驶员可以决定执行突然的操作,这将改变预测的飞机轨迹。在这种情况下,应增加过程噪声。

